Outline of the Studies
Studies in Algebra is a series of explorations in school algebra drawing upon and illustrating the use ofmathematical powers,
mathematical themes
and
pedagogical constructs
for informing the learning, doing and teaching of mathematics.
For more information about these than is in the individual studies, see below.
Each study demonstrates how a single mathematical task can be seen as an example selected from a vast space or domain of related tasks.
Study
1: Up
& Down Sums
or
Why Are We Doing This, Miss?
(Inner &
Outer Aspects of Tasks)
The tasks begin with an invitation to generalise the following
observations
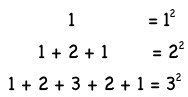
Constructs called upon include
Inner aspects of tasks, in addition to the overt outer aspects
Watch What You Do and Say What You See as pedagogic tactics
Exploiting diagrams when expressing generality
Download pdf file Up & Down Sums last update August 8 2006.
Study
2: Sums To One:
The tasks begin with the question of whether, if someone has chosen two
numbers which sum to one,
which will be the larger:
the sum of the square of the larger and the smaller
the sum of the square of the smaller and the larger.
Constructs called upon include
Dimensions of Possible Variation and Range of Permissible Change
Exploiting Diagrams when expressing generality
Download pdf file Sums To One last update July 11 2006.
The notions of Dimensions of Possible Variation and Range of Permissible Change are exploited both to simplify and then generalise the task.
Download pdf file Marble Sharing last update July 11 2006.
Mason, J. & Johnston-Wilder, S. (2006). Designing and Using Mathematical Tasks. St. Albans: Tarquin.
Mason, J. with Johnston-Wilder, S. & Graham, A. (2005). Developing Thinking in Algebra. London: Sage (Paul Chapman).
Mason, J. & Johnston-Wilder, S. (2004). Fundamental Constructs in Mathematics Education, London: RoutledgeFalmer.
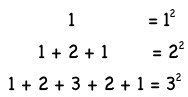
Inner aspects of tasks, in addition to the overt outer aspects
Watch What You Do and Say What You See as pedagogic tactics
Exploiting diagrams when expressing generality
Download pdf file Up & Down Sums last update August 8 2006.
Study
2: Sums To One:
a study in generalisation
The tasks begin with the question of whether, if someone has chosen two
numbers which sum to one,which will be the larger:
the sum of the square of the larger and the smaller
the sum of the square of the smaller and the larger.
Constructs called upon include
Dimensions of Possible Variation and Range of Permissible Change
Exploiting Diagrams when expressing generality
Download pdf file Sums To One last update July 11 2006.
Study 3: Marble Sharing
The tasks begin with a simple, traditional sharing problem:
If Anne gives John one of her marbles, she will then have one more than
twice as many marbles as John then has. However, if instead,
John gives Anne one of his marbles, he will have one more than a third
as many marbles as Anne then has. How many marbles have they
each currently?
The notions of Dimensions of Possible Variation and Range of Permissible Change are exploited both to simplify and then generalise the task.
Download pdf file Marble Sharing last update July 11 2006.
Powers,Themes and Constructs
For the moment, seeMason, J. & Johnston-Wilder, S. (2006). Designing and Using Mathematical Tasks. St. Albans: Tarquin.
Mason, J. with Johnston-Wilder, S. & Graham, A. (2005). Developing Thinking in Algebra. London: Sage (Paul Chapman).
Mason, J. & Johnston-Wilder, S. (2004). Fundamental Constructs in Mathematics Education, London: RoutledgeFalmer.
Mathematical Powers
Mathematical Themes
Pedagogical Constructs
Comments and questions gratefully received
j.h.mason @
open.ac.uk [spaces are there to impede
spam-generating search engines]