0. Introduction
These
pages offer a collection of explorations into properties of
polynomials, starting from the intuitive notion of a chord, and
exploring constructions based on chords.
One of the key ideas is that of multiple ways of thinking about the same idea. For example,
Where possible each section is initiated by an animation. Studying the animation, saying to yourself or to others what you see happening (Say What You See), and locating what is changing and what relationships seem to remain invariant, provides conjectures as starting points for exploration. Applets are available to support exploration in directions that I have thought of, though for maximal learning potential, constructing your own applets brings you into contact with important details and so enriches your appreciation, comprehension and understanding.
Some initiating diagrams and animations
One of the key ideas is that of multiple ways of thinking about the same idea. For example,
- a
graph can be perceived as a geometrical object in its own right, and
as a collection of points, namely {[x, f(x)], x in some interval of R}.
- the
collection of all chords of a polynomial can be thought of either
as a collection of families of chords, each family consisting of all
the chords with a fixed end, or each family consisting of all chords of
a fixed interval width.
Where possible each section is initiated by an animation. Studying the animation, saying to yourself or to others what you see happening (Say What You See), and locating what is changing and what relationships seem to remain invariant, provides conjectures as starting points for exploration. Applets are available to support exploration in directions that I have thought of, though for maximal learning potential, constructing your own applets brings you into contact with important details and so enriches your appreciation, comprehension and understanding.
Some initiating diagrams and animations
| Predict Rational Polynomial | Cubic Tangents | Tangent Power | Chordal Midpoints |
 |
|
|
|
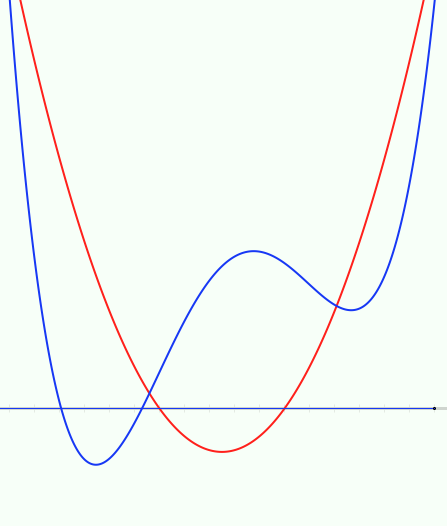
| The red curve is to be the
denominator; the green curve is to be the numerator Predict the graph of their quotient (worksheet) |
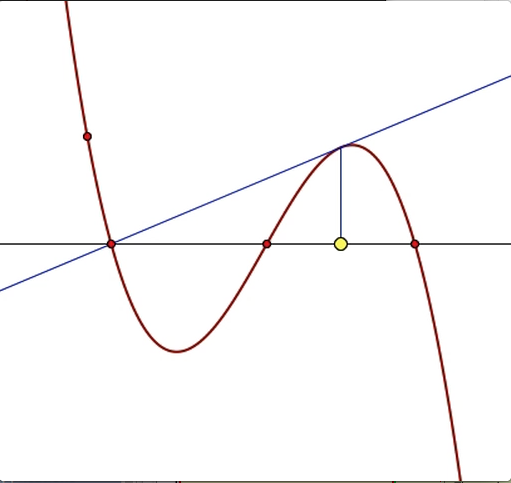
The yellow point is the midpoint
of two of the roots. Link to Animation Download Animation |
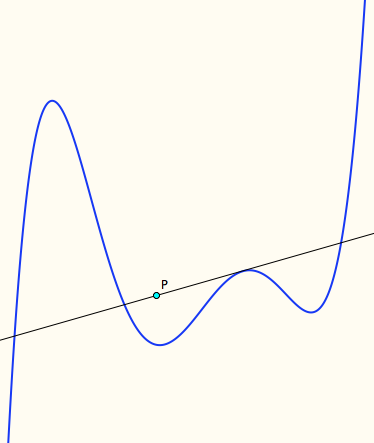
For a given point P, how many
tangents to f go through point P? Describe the regions of constant Tangent Power. Animation Download Animation |
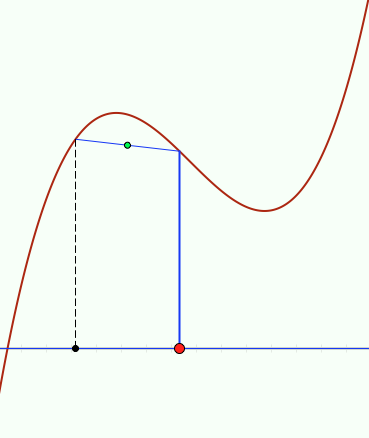
What is the locus of midpoints of all
chords of a cubic? Animation
for Quadratic DownLoad Animation |
| See
Lagrange Polynomials 1.3 |
See
Chord-Based Constructions 2.2 |
See Chord-Based Constructions 2.2 |
1. Lagrange Polynomials
A collection of
explorations introducing Lagrange polynomials (the polynomial of least
degree through a given set of points)
1.1 Predict the graph
1.2 Lagrange Polynomials and Polynomial Coefficients
1.3 Rational Polynomials
1.4 Actions on Graphs (translating, rotating, scaling)
1.1 Predict the graph
1.2 Lagrange Polynomials and Polynomial Coefficients
1.3 Rational Polynomials
1.4 Actions on Graphs (translating, rotating, scaling)
2.
Chord-Based Constructions
A
collection of explorations using constructions on chords:
2.1 Slope and angle
2.2 Parallel Chords & Tangents
2.3 Chordal Gaps
2.4 Chordal Areas
2.5 Chordal SubTangents & SubNormals
2.6 Chordal Circles
2.7 Chordal Parabolae
2.1 Slope and angle
2.2 Parallel Chords & Tangents
2.3 Chordal Gaps
2.4 Chordal Areas
2.5 Chordal SubTangents & SubNormals
2.6 Chordal Circles
2.7 Chordal Parabolae
3. Cobwebs
A collection of explortions of cobwebs involving one or more
functions
3.1 Cobwebs on two functions
3.2 Iteration
3.3 Conjugation
3.1 Cobwebs on two functions
3.2 Iteration
3.3 Conjugation
4.
Mamikon's Theorem
Explorations
of Mamikon's theorem regarding the area swept out by a tangent
4.1 Fixed Length Tangents
4.1 Fixed Length Tangents